Multiview 3D reconstruction

3D reconstruction deals with the problem of recovering 3D geometry from sparse measurements of 2D points. This means that from a set of points in 2D images, taken from different views, we are interested in recovering the actual 3D coordinates of those points.

Lately this problem has received more interest from the industry, with the emergence of checkout-free solutions in retail such as Amazon-Go, Sensei, AiFi or Trigo.

Without loss of generality, in this post we will focus on the reconstruction of 3D points that come from human body joints (or human body keypoints).

We will not discuss the detection of human body keypoints in a 2D image (known as Human Keypoint Estimation). If you are interested you can find more information here.

Problem Definition

Assume that we have a (calibrated) network of $N$cameras $(C_1, C_2, …, C_N)$, each camera captures an image of a human body. After human keypoint estimation, we have access to $K$2D points in each image, as represented in green on image (1). For example, the 2D points in the images provided by camera $C_1$are represented by the matrix $P_{2d}^{C_1} \in \R^{2 \times K}$.

The problem of Multiview 3D reconstruction uses the 2D information present in each camera image $(P_{2d}^{C_1}, P_{2d}^{C_2}, …, P_{2d}^{C_N})$ to reconstruct the 3D points $P_{3d} \in \R^{3 \times K}$ which are represented in red in the image (1).

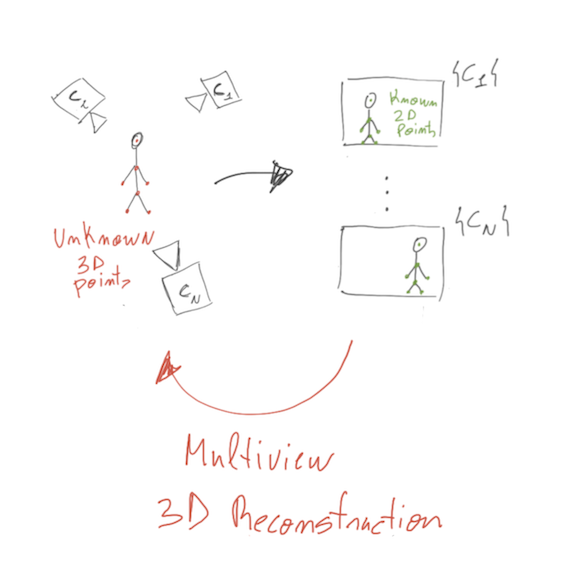
Image 1: Multiview 3D human keypoints reconstruction.

Camera Model

Before discussing how we can perform 3D reconstruction, it is worth to study how is the mathematical formulation of a simple (pin-hole) camera.

A camera is a mathematical transformation that projects points from the 3D world in 2D. For a given 3D point in the camera reference frame, $p_{3d} \in \R^3$ , it can be defined as the function:

$$ f(p_{3d}) = p_{2d} \in \R^{2} = \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \frac{{k_{1}}^T p_{3d}}{{k_{3}}^T p_{3d}} \\ \frac{{k_{2}}^T p_{3d}}{{k_{3}}^T p_{3d}} \end{bmatrix} $$

where $k_1, k_2, k_3 \in \R^{3}$ are the so called camera intrinsic parameters. You can think of them as parameters provided by the camera manufacturer. To learn more about camera intrinsic parameters check here.

The equation above assumes that the 3D point, $p_{3d}$ , is in the same coordinate system as the camera. If we are representing the 3D points in another coordinate system (lets call it $W$ ) we need to know the transformation between that coordinate system and the camera coordinate system. This transformation can be represented by the rotation matrix $ R_{W}^{C} \in \R^{3 \times 3}$ and the translation vector $t_{W}^{C} \in \R^{3}$ . In this case the equation above becomes:

$$ f(p_{3d}^{W}) = p_{2d} \in \R^{2} = \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \frac{{k_{1}}^T (R_{W}^{C} p_{3d} + t^C_W)}{{k_{3}}^T (R_{W}^{C} p_{3d} + t^C_W)} \\ \frac{{k_{2}}^T (R_{W}^{C} p_{3d} + t^C_W)}{{k_{3}}^T (R_{W}^{C} p_{3d} + t^C_W)} \end{bmatrix} $$

By looking at the equations above we see an intrinsic property of a camera: it is impossible to recover the full 3D point coordinates with access to a single observation of a 2D point in an Image.

However, we can solve the above equations with respect to $p_{3d}$ , i.e an undetermined linear system with 2 equations and 3 unknowns ($x, y, z$, which are the coordinates of $p_{3d}$ ), and get a 3D ray which contains all the 3D points that respect the 2 equations.

Stereo Reconstruction

Before discussing the general $N$ views case, we will discuss the scenario where you have $2$ views, i.e two cameras, looking at a 3D point as shown in image 2.

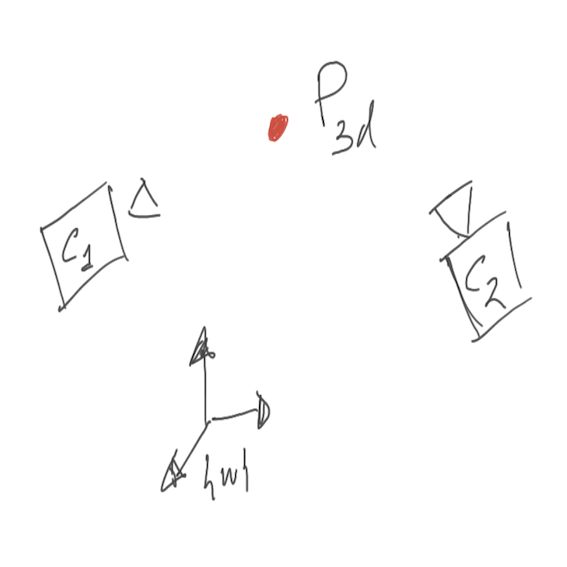
Image 2: Stereo Reconstruction

The equations that we discussed before will be for this case:

$$ p_{2d}^{C_1} = \begin{bmatrix} u_{C_1} \\ v_{C_1} \end{bmatrix} = \begin{bmatrix} \frac{{k_{1}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1})}{{k_{3}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1})} \\ \frac{{k_{2}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1})}{{k_{3}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1})} \end{bmatrix} $$

$$ p_{2d}^{C_2} = \begin{bmatrix} u_{C_2} \\ v_{C_2} \end{bmatrix} = \begin{bmatrix} \frac{{k_{1}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2})}{{k_{3}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2})} \\ \frac{{k_{2}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2})}{{k_{3}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2})} \end{bmatrix} $$

By having access to two views of the same 3D point we can construct a system of 4 equations and 3 unknowns. This overdetermined linear system, $Ax=b$, can be solved in the least squares sense.

To transform the above equations in the form $Ax=b$, we can proceed as follows:

$$ \begin{bmatrix} u_{C_1} {k_{3}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1}) \\ v_{C_1} {k_{3}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1}) \\ u_{C_2} {k_{3}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2}) \\ v_{C_2} {k_{3}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2}) \end{bmatrix} = \begin{bmatrix} {k_{1}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1}) \\ {k_{2}^{C_1}}^T (R_{W}^{C_1} p_{3d} + t_W^{C_1}) \\ {k_{1}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2}) \\ {k_{2}^{C_2}}^T (R_{W}^{C_2} p_{3d} + t_W^{C_2}) \end{bmatrix} $$

$$ \equiv \begin{bmatrix} u_{C_1} ( {k_{3}^{C_1}}^T R_{W}^{C_1} - {k_{1}^{C_1}}^T R_{W}^{C_1} ) \\ v_{C_1} ( {k_{3}^{C_1}}^T R_{W}^{C_1} - {k_{2}^{C_1}}^T R_{W}^{C_1} ) \\ u_{C_2} ( {k_{3}^{C_2}}^T R_{W}^{C_2} - {k_{1}^{C_2}}^T R_{W}^{C_2} ) \\ v_{C_2} ( {k_{3}^{C_2}}^T R_{W}^{C_2} - {k_{2}^{C_2}}^T R_{W}^{C_2} ) \end{bmatrix} p_{3d} = \begin{bmatrix} ( {k_{1}^{C_1}}^T - u_{C_1} {k_{3}^{C_1}}^T ) t_{W}^{C_1} \\ ( {k_{2}^{C_1}}^T - v_{C_1} {k_{3}^{C_1}}^T ) t_{W}^{C_1} \\ ( {k_{1}^{C_2}}^T - u_{C_2} {k_{3}^{C_2}}^T ) t_{W}^{C_2} \\ ( {k_{2}^{C_2}}^T - v_{C_2} {k_{3}^{C_2}}^T ) t_{W}^{C_2} \end{bmatrix} $$

$$ \equiv A p_{3d} = b $$

Which by solving it in the least squares sense gives the 3D point $p_{3d} = (A^T A)^{-1} A^T b$.

Multiview Reconstruction

To generalize the two views scenario to multiple views it will be straightforward. Every view will give us a pair of equations so we can write the following system of equations:

$$ \begin{bmatrix} u_{C_1} ( {k_{3}^{C_1}}^T R_{W}^{C_1} - {k_{1}^{C_1}}^T R_{W}^{C_1} ) \\ v_{C_1} ( {k_{3}^{C_1}}^T R_{W}^{C_1} - {k_{2}^{C_1}}^T R_{W}^{C_1} ) \\ … \\ u_{C_N} ( {k_{3}^{C_N}}^T R_{W}^{C_N} - {k_{1}^{C_N}}^T R_{W}^{C_N} ) \\ v_{C_N} ( {k_{3}^{C_N}}^T R_{W}^{C_N} - {k_{2}^{C_N}}^T R_{W}^{C_N} ) \end{bmatrix} p_{3d} = \begin{bmatrix} ({k_{1}^{C_1}}^T - u_{C_1} {k_{3}^{C_1}}^T ) t_W^{C_1} \\ ({k_{2}^{C_1}}^T - v_{C_1} {k_{3}^{C_1}}^T ) t_W^{C_1} \\ ({k_{1}^{C_N}}^T - u_{C_N} {k_{3}^{C_N}}^T ) t_W^{C_N} \\ ({k_{2}^{C_N}}^T - v_{C_N} {k_{3}^{C_N}}^T ) t_W^{C_N} \end{bmatrix} $$

Again, this system of $2N$ equations and $3$ unknowns can be solved in the least squares sense.

Since we assumed that we have a calibrated camera network, that means that we have access to the parameters $R_{W}^{C_i}, t_{W}^{C_i}, k_1^{C_i}, k_2^{C_i}, k_3^{C_i}$. $R, t$ are the so called extrinsic parameters and $k_1, k_2, k_3$ the intrinsic parameters. To learn more about how to obtain these parameters you can check here.

Now that we know how to solve 3D reconstruction given multiple views for a single 3D point, we can apply it to reconstruct $K$human body keypoints given its 2D measures in different images.

Since we have $K$human body keypoints, we simply need to construct $K$ of the systems of equations presented before:

$$ A^1 p_{3d}^{1} = b^1 \\ … \\ A^K p_{3d}^{K} = b^K $$

All of these systems can be solved in parallel since they are all independent and we would recover all the $P_{3d} \in \R^{3 \times K}$ points.