An ordinal classification loss - part 2
Published on
In the last blogpost, I explained how the usage of torch.argmax function can lead to issues regarding the gradients of the loss function:
Even though this loss function has the desired properties such as increasing the loss for cases where the ordinal nature of the output is more violated, its gradients don’t change making the updates of the model not aware of that ordinal nature.
In this blogpost, I will propose an alternative to this loss function that solves the issues regarding the gradients.
Let’s start by generalising the loss above:
we can interpret $R(p(\hat{y} | x), y)$ as a regularisation function that depends on the model output and the label. This regularisation should have some important properties such as differentiability (almost everywhere) wrt model parameters. It should also capture the ordinal nature of our labels, i.e $y=1 < y=2 < y=3 < y=4 < y=5$ .
The simplest choice one can think is a linear function of the model output $p(\hat{y}|x)$ with a constant $w_y$.
This function is clearly differentiable wrt model parameters, remember that $p(\hat{y}|x)$ depends on your model parameters. In addition, we tweak ${w_{y}}$ to make it capture the property of being aware of our labels ordering.
Imagine the scenario previously discussed of review rating prediction where we should predict a score (1-5) for each user review. In this scenario $p(\hat{y}|x) \in \mathbb{R}^{5}$ and so will $w_y$.
For a specific example in our dataset if $y=1$ and $w_{y=1} = [0, 1, 2, 3, 4]$ then our regularisation will penalize more if our probabilities are less concentrated around $y=1$ .
In general, we can describe the different $w_y$ as rows of a matrix that has the following structure:
where $i$ is the identifier of the row and $j$ the identifier of the column.
We can then write the final loss function $l_{doce}$ ($doce$ stands for differentiable ordinal cross entropy) as:
where $w_y$ represents the row of the matrix $W$ indexed by the corresponding label $y$.
It is also fairly easy to implement this loss function in torch:
def _create_weight_matrix(num_classes: int) -> torch.Tensor:
W_matrix = []
for i in range(num_classes):
W_matrix.append([abs(i - j) for j in range(num_classes)])
return torch.tensor(W_matrix)
def diff_ordinal_cross_entropy(
input: torch.Tensor,
target: torch.Tensor,
alpha: float = 1,
reduction: Optional[str] = "mean",
) -> torch.Tensor:
num_classes = input.shape[1]
weights_matrix = _create_weight_matrix(num_classes)
ce = torch.nn.functional.cross_entropy(input, target, reduction="none")
prob = torch.nn.functional.softmax(input, dim=1)
reg = weights_matrix[target, :] * prob
reg = reg.sum(dim=1)
loss = ce + alpha * reg
if reduction is None or reduction == "none":
return loss
if reduction == "sum":
return loss.sum()
if reduction == "mean":
return loss.mean()
(Implementation of $l_{doce}$ in torch)
We will see some examples of the output of this loss function using the same scenarios as in the previous blogpost:
This means that for $x_1$ the model puts more probability in the review score 5, for $x_2$ in 1 and for $x_3$ in the review score 2.
If we assume that the label for all the examples should be the review score 1, the value of $l_{doce}$ for each of the examples is:
which confirms that our loss is capturing the ordering between our labels since it is giving a bigger loss in $x_1$ then $x_3$ and finally $x_2$ .
Another issue seen in the previous blogpost is that the gradients of $l_{oce}$ and $l_{ce}$ were in fact the same which would turn out in the same updates in the model parameters while training. If we check the gradients for our new loss function (in the same examples discussed above):
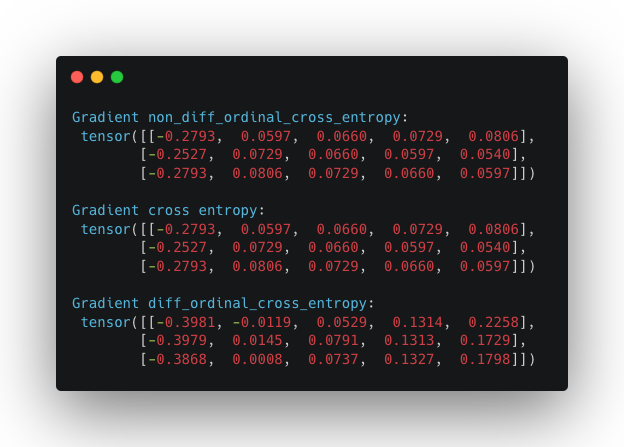
we see clearly that the gradients of $l_{doce}$ are different from $l_{ce}$ and $l_{oce}$ which proves that our loss will in fact make the model parameters be updated differently from $l_{oce}$ and $l_{ce}$.
With this simple modification, we arrived at a loss function that has both properties:
- It is higher when our output probability doesn’t respected the natural ordering of the labels
- It is differentiable and its gradients are different from the normal cross entropy loss
You can find the code used in this blogpost here.
Hope you had fun, thanks for reading :)