An ordinal classification loss - part 1

Many times we find ML problems that can be approached as classification, but after digging into it, we notice that there are hierarchical or ordering relationships between our classes.

For example, imagine that you are doing review rating prediction. Given an user review you want to give it a score from 1-5. An approach might be to see the problem as a text classification where there are 5 classes, one for each of the possible ratings.

For the sake of simplicity imagine that your text is simply represented by an embedding vector $x \in R^d$. One can use a simple model such a linear classifier given by the function $F(x) = softmax(Wx + b)$, where the model parameters are the matrix $W \in R^{5 \times d}$ and the vector $b \in R^5$.

This model is predicting a probability distribution $p(\hat{y}|x$) across every possible rating $[1, 2,3,4,5]$.

class SimpleLinearClassifier(torch.nn.Module):
    def __init__(self, input_dim: int, num_class: int) -> None:
        super().__init__()
        self._linear = torch.nn.Linear(input_dim, num_class)

    def forward(self, x: torch.Tensor) -> ClassificationOutput:
        logits = self._linear(x)
        prob = torch.nn.functional.softmax(logits)
        return ClassificationOutput(logits, prob)

(A simple linear classifier in pytorch.)

These models are usually trained using the cross entropy loss. In our case for a dataset (or a batch) of size $N$ it is given by:

$$ L[(x_{1},y_{1}), … , (x_{N}, y_{N})] = \frac{\sum_{n=1}^{N} \space l_{n}}{N} \\ = \frac{\sum_{n=1}^{N} CE(p(y_n), p(\hat{y_n}|x_n))}{N} \\ = \frac{ \sum_{n=1}^{N} \sum_{k=1}^{5} -p_{y_n}(y=k) \space log(F_k(x)) }{N} \\ = \frac{\sum_{n=1}^{N} \space - log(F_{y_{n}}(x))}{N} $$

where $ F_{y_{n}}(x) $ represents the $y_{n}$ entry of the output probability, also bear in mind that $p_{y_n}(y=k)$ is 0 everywhere and 1 when $y=y_n$.

Now that we know the formula of the loss lets see some examples. Imagine that the output of your model is something as follows:

$$ F[x_1] = softmax([0.1, 0.2, 0.3, 0.4, 0.5]) \\ F[x_2] = softmax([0.5, 0.4, 0.3, 0.2,0.1]) \\ F[x_3] = softmax([0.1, 0.5, 0.4, 0.3, 0.2]) $$

This means that for $x_1$ the model puts more probability in the review score 5, for $x_2$ in 1 and for $x_3$ in the review score 2. If we assume that the label for all the examples should be the review score 1 and we compute the loss for each of the examples we get the following values:

$$ y_1=1, l_1=1.8194 \\ y_2=1, l_2=1.4194 \\ y_3=1, l_3=1.8194 $$

Looking at this values we arrive at a funny conclusion, even though in our problem it makes sense that we would have a bigger loss in the example 1 compared with the example 3, it doesn’t happen. The cross entropy loss doesn’t have into account the ordering in our classes, i.e 1 < 2 < 3 < 4 < 5.

The question that stands now is: “How can we make our loss take into consideration the natural order of the review ratings ?”

After some “googling” we came across this implementation of a regularisation to make the CE loss aware of the ordering of the classes, in summary it can be described as the following equation:

$$ l_{oce} = CE(p(y), p(\hat{y}|x)) + \alpha | \underset{\hat{y}}{\arg \max} \ p(\hat{y} | x) - y | $$

This loss can be easily implemented in pytorch:

ce = torch.nn.functional.cross_entropy(input, target, reduction="none")
reg = target - input.argmax(dim=1)
reg = torch.abs(reg)
loss = ce + alpha * reg

(Torch example of the proposed ordinal cross entropy. For more details check here.)

Looking at the output of the new loss for the example above we se that we have the desired behaviour:

$$ y_1=1, l_1=5.8194 \\ y_2=1, l_2=1.4194 \\ y_3=1, l_3=2.8194 $$

making the loss higher when the prediction is more distant from the label.

At a first glance, one might think that with this loss we accomplished our goal and we can now put our model training and have great results…. However, we need to take a closer look of what happens with the gradients of this new loss.

The first part of the loss is fine since is the standard cross entropy however, the second part might cause problems. Think a bit of how one would calculate the gradient of $\arg \max$ with respect to the model parameters.

In fact, the $\arg \max$ might not even be differentiable making it difficult to calculate gradients. For an in depth mathematical analysis regarding $\arg \max$ please check this paper from the (awesome) SARDINE NLP group in Lisbon.

To check the gradients we do a simple test with torch using the same data as in the previous examples.

logits_ce = torch.tensor(logits.numpy(), requires_grad=True)
loss_ce = cross_entropy(logits_ce, labels, reduction="mean")
loss_ce.backward()
grad_ce = logits_ce.grad

logits_oce = torch.tensor(logits.numpy(), requires_grad=True)
loss_ordinal_ce = non_diff_ordinal_cross_entropy(
    logits_oce, labels, reduction="mean", alpha=1
)
loss_ordinal_ce.backward()
grad_oce = logits_oce.grad

(Torch example to compute gradients, for more detail check github.)

We arrive at the conclusion that the gradients of the two losses (computed according to torch automatic differentiation) are in fact the same:

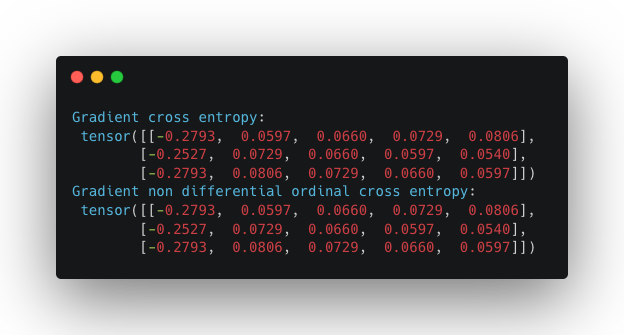
This poses a challenge since even though the loss is capturing what we want, the gradients are not and that will make the updates on the model parameters unaware of the ordering structure.

In the 2nd part of this blogpost we will see how to solve this issue by introducing another type of regularisation that doesn’t have the non differential issue but still captures the ordering relationships of our classes.

You can find the code used in this post here.

Thanks for bearing with me and my awful math notation. See you soon :)

Acknowledgements

Most of the ideas present in this blogpost are a result of discussions with my work colleague Ivo Silva.